CodeIQ「バイバイマンを数えよう」

最近 CodeIQ でいろいろな問題に挑戦しているんですが、今回コードゴルフ問題に挑戦してみました。
（ちなみに CodeIQ のほうでは「むぎゅう」名義で活動してます）

勉強がてら Ruby で挑戦です。javascript だと巨大数とか出てきたときにめんどいし……。
あとコードゴルフ問題で console.log(hoge) とか書くのやだし……。

それはさておき。

問題は現在は CodeIQ で参照することは出来ませんが、近いうちに出題者の方の解説ページが公開されると思われます。

問題の内容はざっくりと以下の通り。

バイバイマンは以下のような性質を持ちます。

1. 1日経過するとサイズが倍になります。
2. サイズが 10 を超えると分裂します。
3. 分裂後のサイズは分裂前のサイズの 10 の位の数と 1 の位の数になります。

具体的には、

1日目	2日目	3日目	4日目	5日目	6日目
1	2	4	8	1, 6	2, 1, 2

のように変化していきます。

【問題】
バイバイマンの数を1日ごとに調べて、1日目から100日目までを出力してください。

結果は 40byte で Ruby の中では上から3番めのサイズでした。 自分的にはなかなかの出来で満足……いやちょっと悔しいですけど。
40byte 切りの方たちのコードがどんな感じか見るのが楽しみです。

とりあえず自分が提出したコードとそこに至るまでの過程を解説とかしてみたいと思います。

結論だけ見たい方はこちら

素直に数えてみる

まず、問題の通りに素直にバイバイマンを数えると以下のような感じになるでしょうか。

# サイズが size のバイバイマンが rest 日後に何匹になっているかカウントする
def count_baibaiman(size, rest)
    count = 1
    while rest > 0
        rest -= 1
        size *= 2
        if size >= 10 then
          count += count_baibaiman(size%10, rest)
          size /= 10
        end
    end
    return count
end

# 1日目から100日目までのバイバイマンの数を表示
100.times{|i| p count_baibaiman(1,i) }

まあ、このままだとすぐにスタックオーバーフローになりそうなので、メモ化とかが必須になりますね。

少し工夫してみる

さて、先のコードはある程度汎用的になるように考えましたが、今回の問題に特化して考えてみると、バイバイマンの初期値がサイズ 1 が 1 匹なので、そのサイズの移り変わりは以下の図のような感じ。

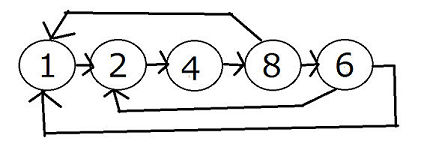
このようにバイバイマンの取りうるサイズは 1,2,4,8,6 の 5 種類しかありません。 というわけで、この図をそのままコードに落としたら以下みたいになります

# b はバイバイマンの各サイズの数を収めた配列
# Array#rotate! を使いたい関係でサイズ 6,8,4,2,1 の順で配列に入れてる
b=0,0,0,0,1
100.times{
    p b.inject(:+)	# 全てのサイズの数を合計して表示
    b.rotate!	# 各サイズの数を次のサイズに移動
    b[3]+=b[4]	# サイズ 2 の数に1世代前のサイズ 6（現世代でサイズ 1）の数を足す
    b[4]+=b[0]	# サイズ 1 の数に1世代前のサイズ 8（現世代でサイズ 6）の数を足す
}

コメントとかインデントとかいろいろ省くと

b=*[0]*4,1;100.times{p b.rotate!.inject(:+);b[3]+=b[4];b[4]+=b[0]}

一応これで 66byte になります。

数学っぽく考えてみる

ここから、さらにアルゴリズムを見直します。

先のバイバイマンのサイズの遷移図を見ると分かる通り、n 世代目のバイバイマンの数は n-1 世代目の合計に n-1 世代目のサイズ 8, 6 の数を足したものになります。 ここで n 世代目の全てのバイバイマンの数を f(n)、n 世代目のサイズ s のバイバイマンの数を b[s](n) とすると、

f(n) = f(n-1)+b[8](n-1)+b[6](n-1)	… ※1

の関係が成り立ちます。ここで b[6](n) = b[8](n-1) ですから、※1式は

f(n) = f(n-1)+b[8](n-1)+b[8](n-2)	… ※2

となります。
ここで b[8](n) について考えると、

b[8](n) = b[2](n-2)
        = b[1](n-3)+b[6](n-3)
        = b[6](n-4)+b[8](n-4)+b[8](n-4)
        = b[8](n-5)+2*b[8](n-4)

となりますので、これを※2 式につっこんで、

f(n) = f(n-1)+b[8](n-6)+2*b[8](n-5)+b[8](n-7)+2*b[8](n-6)	… ※3

が導かれます。
ところで ※2 式より

f(n)-f(n-1) = b[8](n-1)+b[8](n-2)

ですから、※3 式を変形して

f(n)-f(n-1) = 2*(b[8](n-5)+b[8](n-6))+(b[8](n-6)+b[8](n-7))
            = 2*(f(n-4)-f(n-5))+(f(n-5)-f(n-6))				… ※4

この※4 式をさらに変形すると

f(n)-2*f(n-4)-f(n-5) = f(n-1)-2*f(n-5)-f(n-6)				… ※5

が得られます。というわけで g(n)=f(n)-2*f(n-4)-f(n-5) とすると、

g(n) = g(n-1)

なので、

g(n) = A	# A は定数

ここで

g(5) = f(5)-f(1)-f(0) = 2 - 1 - 1 = 0

なので、A = 0 となり、

f(n)-2*f(n-4)-f(n-5) = 0

つまり

f(n) = 2*f(n-4)+f(n-5)			… ※6

が導かれます。

…実際には最初からこんなめんどくさい変形をしたわけじゃなくて、※4 式の時点で g(n)=f(n)-f(n-1) とおいて、g(n)=2*g(n-4)+g(n-5) を計算してたんだけど、この関係式って f(n) そのものについても成り立つんじゃね？と思いついて、実際に値を突っ込んだらなんかうまくいった、という感じです。
証明とかは完全に後付けですね。

ともかく、これを実際にコードに書くと

# バイバイマンの数を格納する配列
# 初期値は 1,1,1,1,2
f=1,1,1,1,2
100.times{
    p f[-5]		# バイバイマンの数の表示
    f<<2*f[-4]+f[-5]	# ※6 式の通りに5世代後のバイバイマンの数を計算
                        # 計算結果は f に全部 push する
}

コメントとかインデントとか省いて、

f=*[1]*4,2;100.times{f<<2*f[-4]+p(f[-5])} # 41byte

これで一気に 41byte。
ここからさらに一工夫。 ループ内で取り出した f[-5] の値は次のループでも使うのでこれを変数に突っ込んでおきます。

f=*[1]*4,2;100.times{f<<p(c)+2*c=f[-5]}	# => error

これだと 変数 c が未初期化なのでエラー。というわけで、

f=c=*[1]*4,2;100.times{f<<p(c)+2*c=f[-5]} # 41byte

変わりませんね。
ここで配列 f そのものは 4 世代前までしかアクセスしないんだから、 初期化時に 5 世代分持ってる必要はないことに気づきます。
ただし、情報としては 5 世代分必要なので c に 5 世代前の情報を突っ込んでおくことにします。

f=c=*[1]*3,2;100.times{f<<p(c)+2*c=f[-4]} # 41byte

まだ変わらない。初期化にもうちょい工夫したい。
というか今は f(0)=1 から f(4)=2 までの情報を持っているわけですが、 ※6 式から

f(-1)=f(4)-2*f(0)=0

が導けるわけだから、c には f(-1)=0 を突っ込むことにします。
ただし、今までは c の値を表示していたのを f[-4] の値を表示することに注意

c=0;f=[1]*4;100.times{f<<c+2*c=p(f[-4])} # 40byte

というわけで 40byte。これが提出したコードになります。

悪あがいてみる

いろいろと小細工

c の初期値が 0 なのでこれをどこかから持ってこれないかと思ったんですが。
一番有力候補だったのが、組み込み変数 $.。
これは標準入力から読み込んだ行数が格納されている変数で、ruby の起動時には 0 が入っています。 さらになぜか任意の Fixnum を代入できるという。なんで代入できるんでしょう？
ともかく、これを利用すると、

f=[1]*4;100.times{f<<$.+2*p($.=f[-4])} # 38byte … NG

となり 38byte。すばらしい！

と思ったんですが、ダメ。
$. に代入できるのはあくまで Fixnum であり、Bignum は代入できないのでした。無念。

ほかにも、

f=[1]*4;-99.upto(c=0){f<<c+2*p(c=f[-4])} # 40byte

とか、

f=[-~c=0]*4;100.times{f<<c+2*p(c=f[-4])} # 40byte

とか、

c=0;f=[1]*4;96.times{f<<c+2*c=f[-4]};p *f # 41byte

とか、

f=c=1,1,1,2;100.times{c,*f=f<<p(c)+2*f[0]} # 42byte

とか小細工してみたけど、ことごとくだめでした。

個人的に面白いものが書けたと思ったコード。

eval"(f=[1]*4)<<"+"+2*p(c=f[-4])<<c"*100 # 40byte

ループを文字列で組み立てて eval するというパターン。
c の初期値は 0 なので 1 ループ目で c を足す必要はなく、1ループ目で c の初期化をしているので 2ループ目以降で問題なく c を参照できるということを利用しています。
結構面白いと思ったんだけど、40byte から縮まず。残念。

Enumerable#map を使ってみる

c=0;f=[1]*4;25.times{f.map!{|x|c+2*p(c=x)}}	# 43byte

配列には 4 世代分だけ入ってればいいから、参照したら map! でがしがし書き換えていく。 配列にアクセスするための [] がなくなってきれい。

さらに文字列ループを使うと、

c=0;eval"([1]*4)"+".map{|x|c+2*p(c=x)}"*25	# 42byte

配列に f という名前を付ける必要がなくなりました。 また元の配列自体を書き換える必要がないので、map! が map になったのも嬉しい。 文字列ループとメソッドチェーンの相性よすぎです。
長さは 42byte で提出したコードより長いですが。個人的にかなりお気に入り。

さらに数学っぽく考えてみる

もう詳しい解説は書きませんが、※6 の漸化式の特性方程式を解くことにより

f(n)=f(n-1)-f(n-2)+f(n-3)+f(n-4)

が導かれます。
f の値を 4 世代分だけ記憶しておけばいいから短くできそうですが、 実際の計算に 4 世代分すべての値を使うので、計算式自体が長くなってしまいます。 配列に突っ込んだら [] の量がすごいことになるので、全部 1 文字変数で記憶する方針で。

a=b=c=d=1;100.times{d=p(a)+(a=b)-(b=c)+c=d}	# 43byte

式途中の代入の括弧が大量にあるので、ちょっと一工夫。

p a=b=c=d=1;99.times{d=a+p(a=b)-(b=c)+c=d}	# 42byte

p で表示する変数を 2 項目(f(n-3))にすることで、p で必要な括弧と代入に必要な括弧をまとめています。一番最初の数字だけは別に出力する必要があるので、変数の初期化時に。おかげで 100 回ループが 99 回ループになって 1byte 減りました。でも、42byte。40 の壁は高かった……。

感想

まともにコードゴルフに挑戦するのも初めてでしたし、そもそも Ruby 自体今年に入ってから勉強始めたようなものなのでなかなかに大変でしたが、Ruby のリファレンスマニュアルとずっとにらめっこしたり、多重代入の挙動に悩んだり、多項漸化式の解き方ってどうするんだっけ？と昔の教科書引っ張りだしたりする日々は楽しかったです。

次回もなにかあれば挑戦してみるかなあ。